乱射ボーイ(仮) - イオン光学ベースのビーム像モンテカルロシミュレータ　のページ

12/24
ひとまず最低限の仕様を満たした状態になった。
HBOOK出力は未実装。しかも実装するのが非常に面倒らしいということが判明しゲンナリ。
中村さんに相談して、とりあえずROOTをインストールした。
あと、乱射ボーイから Backhands に改名します。心の中ではずっと乱射ボーイだけどな。

12/23
予想外に梃子摺ったが、マトリクス読み込み処理を書き終える。コードの汚さに軽く絶望するが、 とりあえず動かすところまで持っていかねば。明日こそ。

系の転送行列およびビームの粒子と分布を与えると、その系の終端で見えるビームの像を出力する。
言い替えると、ビームの初期位相空間を系の転送行列で変換した結果を出力する。

C++で記述。数値計算ライブラリ Blitz++ を使う。

入力

COSY Infinity のPMコマンドの結果をそのまま使えるようにする

出力

プレーンテキスト、HBOOKを必要に応じて選べるように。

トランスファーマトリクスは、磁石などの要素による荷電粒子ビームへの作用を表現する行列(テンソル) である。 形式的な定義を一言で言えば、粒子のパラメータをベクトルで表したときの、そのベクトルのマクローリン展開係数である。

位相空間をm次元とするとき、n次のトランスファーマトリクスはm次元のn+1階テンソルとなる。
0次マトリクス(＝ビームセンターベクトル)は普通ゼロベクトルに取る。

位相空間を5次元(x,a,y,b,d)とし、2次のマトリクスM_{ijk}(3階テンソル)を例にとる。
この時、このマトリクスによる2次の寄与は

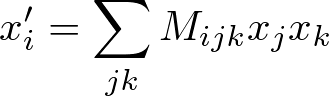
となる。 これを見ると、3つの添字のうちj,kは対称であることがわかる。
従って、独立な成分は 5*(5+2-1)!/4!2! = 75個しかない。
より高次のマトリクスでもこの事情は変わらない。つまり2番め以降の添字は全て対称であるから、m次元・n次のマトリクスは m*(m+n-1)!/(m-1)!n!個の独立な成分を持つ。
COSY Infinity のPMコマンドは独立な成分だけを出力する。

オーダー3次の出力例
各行はエレメントと位置指定用数列から構成される。
最初にスペースを1つ空けて、14文字の数値が5セットあり、これがエレメント部である。
その後で、エレメント部の各カラムがトランスファーマトリクスのどの成分に対応するのかを決める数列がある。 これは長さ6の整数列である。
注意すべきは、この時位相空間は6次元なのにエレメント部は5カラムしかないことである。 オミットされたのは第5成分t(時間)に対する寄与の項である。 時間に対する寄与は無いが、時間からの寄与は1次のみ出力されることに注意しよう。 本プログラムでは時間に関する項は完全に無視する。

さて、位置指定数列の見方に戻る。これは例をあげて説明する。
たとえば、数列が021000だった場合。桁の合計は3であるが、これはこの行が3次のマトリクスの成分を表している事を意味する。 具体的に言えばM_{i223}である。iはカラム番号であり、右から1〜6となる。5は前述のとおり時間なので無視する。 つまり、この行のカラムは
M_{1223} M_{2223} M_{3223} M_{4223} M_{6223}
と並んでいる。
また前述の通り、M_{i223}はM_{i232}でありM_{i322}でもあるので、この行は実質的に15成分を表している。

accend->works->labnote->index page